Fractions, decimals and percentages are types of ratios. Ratio is a term that describes how numbers relate to each other. You can further your understanding of ratios by going to our Ratio page. In short, fractions, decimals and percentages are ways of describing part of a whole.
Think about pouring a glass of squash. You are likely to use 25% cordial with 75% water. The equivalent decimal would be 0.25 cordial and 0.75 water. As a fraction, we would have 1/4 cordial and 3/4 water. You use fractions, decimals and percentages daily, probably without realising. You use them when you:
split a bill in a restaurant
order a product for your company
follow a recipe
make a cocktail
share food
calculate a discount
work out medical dosages
analyse and compare data.
Working through this page will help you:
understand how to read fractions
add and subtract fractions
convert fractions, decimals and percentages
work out increases and decreases in percentages.
Understanding fractions, decimals and percentages
Use the following explanations and activities to check your basic understanding of fractions, decimals and percentages. You will need this understanding to complete activities and find solutions to questions on your course.
What is a fraction?
A fraction is a part of a whole number divided into equal parts. The top number is the numerator, which represents the number of parts of a whole. The bottom number is the denominator, which represents how many equal parts the number was divided into.
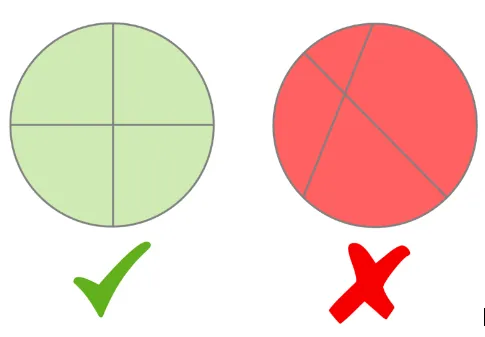
Click on the hotspots in the image below.
Tip:
You can only have a fraction with equal parts. See the picture below. The circle on the left is divided into 4 equal sections. So, if we wanted 1 part of this circle, it would be ¼. However, the circle on the right is not in equal parts, so we cannot say one section is ¼.
The different types of fractions are explained in the table below. You need to know the various types as you will probably have to convert them to add and subtract fractions. Knowing the basics of fractions will allow you to develop more advanced mathematical skills.
| TYPE OF FRACTION | DEFINITION | EXAMPLE |
|---|---|---|
| Proper fraction | The numerator is smaller than the denominator. | 2/5 |
| Improper fraction | The numerator is larger than the denominator. | 8/3 |
| Mixed fraction | A whole number plus a fraction | 6 1/2 |
| Like fraction | Fractions with the same denominator. This is important for arithmatic. | 7/9 and 4/9 |
| Unlike fraction | Fractions with a different denominator. This is important for arithmatic. | 6/7 and 2/3 |
| Equivalent | Fractions that are of equivalent value. | 1/3 and 2/6 |
What is a decimal?
‘Decimal’ means ‘based on 10’, just like percentage is based on 100.
Think of a decimal number as those numbers that are in between whole numbers. For example, 10 and 11 are whole numbers and 10.5 is between them. The first component of 10.5 is the whole number (10), and the second component is the fractional part (.5). One of the most common uses of decimals is with money, such as $6.99.
The simplest way to read a decimal is to read the whole number like normal, read the decimal point as ‘point’ and then read each digit after the point as an individual number. E.g. 3.125 would be read as three point one two five.
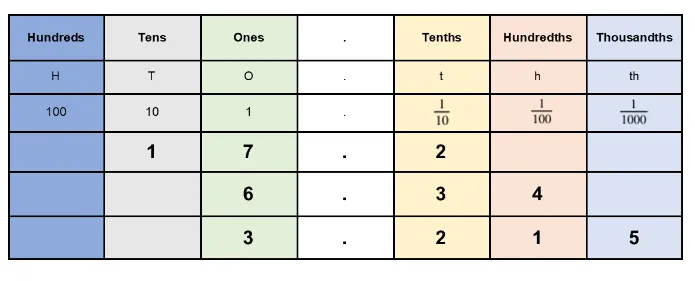
The easiest way to visualize a decimal is by looking at a place value chart. As we move from left to right, the value decreases by 1/10.
Rows 1 - 3: these rows express what each digit represents mathematically.
Rows 4 - 6: these rows have examples of how we place decimal numbers into the chart.
Practice reading these aloud.
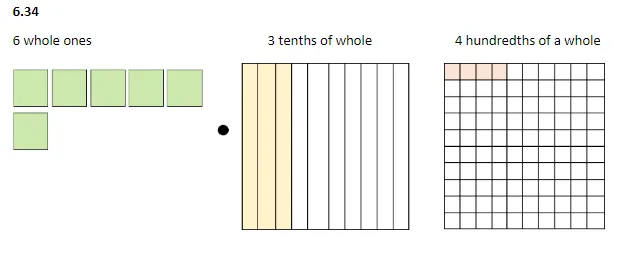
Let’s look at how we can visualize these decimals. Ones are represented by a whole block. Tenths are represented by a whole block divided into ten. Hundredths are represented by a whole block divided into a hundred. This trend continues on. We then shade how much of each column we have to get a visual representation of our number.
The first number we have is 17.2. This means we have 17 whole ones, and 2/10ths. This also looks like this.
Next, we have 6.34. This time we’ve had to add the hundreds chart as 4 is in the hundredth's column.
What is a percentage?
Percent means out of 100 and is represented by the symbol %.
The easiest way to visualize a percentage is by using a 100s square. As percentages are out of 100, we count the number of boxes that are shaded to get the percentage.
- Look at our box on the left. You can see 50 shaded boxes, so the percentage should be 50%. Click on the hotspot to check.
- Work out the next two percentages and click on the hotspot to reveal the answer.
Using fractions, decimals and percentages
This section introduces you to different ways you may use fractions, decimals and percentages.
Adding and subtracting fractions
The video below gives an introduction to adding and subtracting fractions.
The most important thing to remember is that they must have the same denominator. This can involve having to find a common denominator, which is further explained in the video.
Calculating percentage increases and decreases
This video and practice questions are designed to give you the knowledge and formulas to be able to work out percentage increase and decrease both with and without a calculator.
Try these review tasks to check your understanding. Remember, it is OK to use a calculator!
Calculating percentages of a quantity
Because a percentage is out of 100, we can work out the percentage of a number simply by dividing by 100 and multiplying by the total quantity.
Look at this example.
Mountain primary School has 209 children. Of those, 34% of the children take the bus. How many children do NOT take the bus?
You can work this out in two ways.
Method 1
The percentage we are trying to find is 34%. We take this 34% and divide it by 100. We then multiply this answer by our total quantity which is 209, to get 34%.
34% ÷ 100 = 0.34
0.34 x 209 = 71 children
However, this gives us the answer for the total amount of children who take the bus. Our question wants us to find out how many children do not take the bus. Therefore, we must take 71 away from 209.
209 – 71 = 138.
So, 138 children do not take the bus to school.
Method 2
The second way to work it out is to find out the percentage we need to start. We know that 100% is total, so 100 - 34 = 66%. We are looking for 66% of 209. Now we can use the same equation as before.
66% ÷ 100 = 0.66
0.66 x 209 = 138
We get the same answer, 138 children.
The relationship between fractions, decimals and percentages
This section further explores fractions, decimals and percentages.
Watch
The videos below explain how to convert fractions, decimals and percentages. Pay attention as they take you through some examples. After you watch, do some review tasks to check your understanding.
Take a break and think about what you have learned. When you are ready, watch the next video.
Knowing how to convert between the three is a useful skill because they are often used in different situations. You might cut a chocolate bar in ½, you might have $0.50 in your purse, and you might buy an item at 50% discount. Although they are represented differently, they all have the equivalent value: half.
Converting between the three ratios will allow you to change the format of a question. This can result in easier calculations. It might be easier to find ¼ of a number, than 25% as you know instantly that you just need to divide by 4.
Check your understanding
Think about what you have learned and try these tasks to check your understanding.
Practice
As we have discussed, it is important to be able to switch between fractions, percentages and decimals. Work through the tasks below. They are similar to things you will have to do in real life.
Drag the answers into the correct place on the chart. Once you have completed the chart, you might notice a pattern to the conversions.
Try these conversions.
We value your opinion. Please click on the button to share your feedback on these materials. |
Did you know CDU Language and Learning Advisors offer a range of study support options?
https://www.cdu.edu.au/library/language-and-learning-support